數(shù)據(jù)結構分類以及數(shù)據(jù)結構特點——優(yōu)缺點
作者:微風01
數(shù)據(jù)結構知識點整理數(shù)據(jù)是信息的載體,是描述客觀事物的數(shù)、字符、以及所有能輸入到計算機中,被計算機程序識別和處理的符號數(shù)值、字符等的集合。

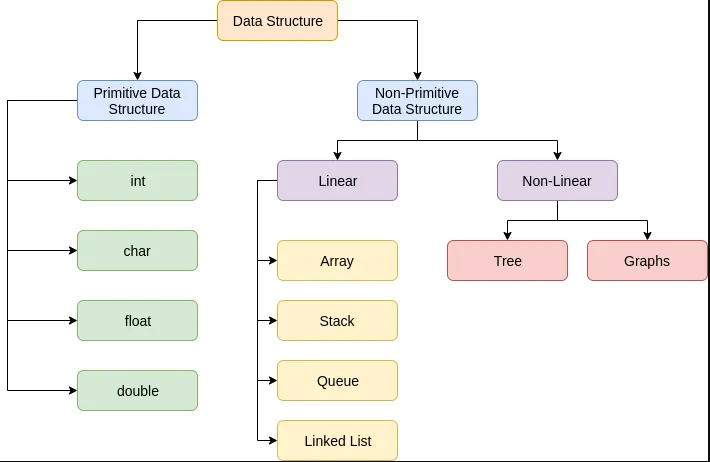
數(shù)據(jù)結構分類
數(shù)據(jù)結構是計算機中組織和存儲數(shù)據(jù)的方式。
數(shù)據(jù)結構分類-原始與非原始
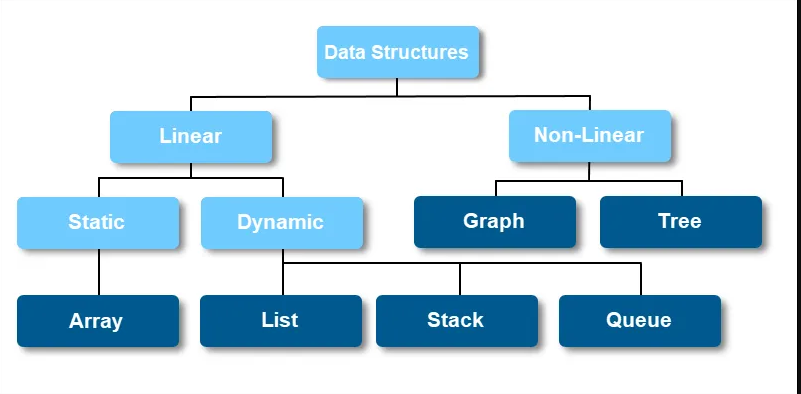
數(shù)據(jù)結構分類-線性與非線性
原始數(shù)據(jù)結構
基本數(shù)據(jù)結構不能進一步劃分。
- 具有算術運算的 8 位整數(shù)(字節(jié))— 最小值為 -128,最大值為 127(含)。
- 具有算術運算的 16 位整數(shù)(短整型)— 最小值為 -32,768,最大值為 32,767(含)。
- 具有算術運算的 32 位整數(shù) (Int) — 最小值為 -231,最大值為 230。
- 具有算術運算的 64 位整數(shù)(長整型)— 最小值為 -263,最大值為 262。
- 16 位 Unicode 字符/字母數(shù)字字符/符號 (char) — 最小值'\u0000'(或 0)和最大值'\uffff'(或 65,535(含))。
- 帶算術運算的單精度 32 位 IEEE 754 實數(shù)(浮點型)。
- 帶算術運算的雙精度 64 位 IEEE 754 實數(shù) (Double)。
- 布爾值(具有邏輯運算(布爾)的值 { true, false} 的集合 - 只有兩個可能的值:true和false。
非原始數(shù)據(jù)結構
- 數(shù)據(jù)結構可用于其他復雜的存儲。
線性
- 元素組成一個序列
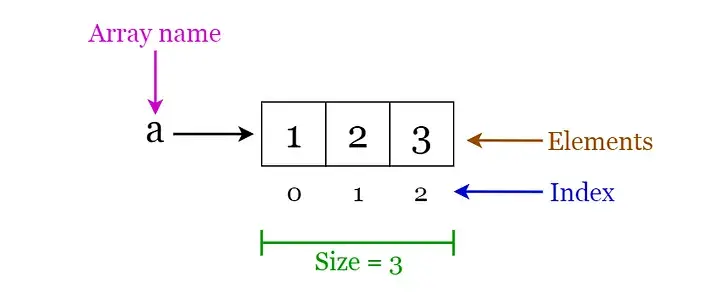
數(shù)組(Array)
- 它是相同類型元素的集合。
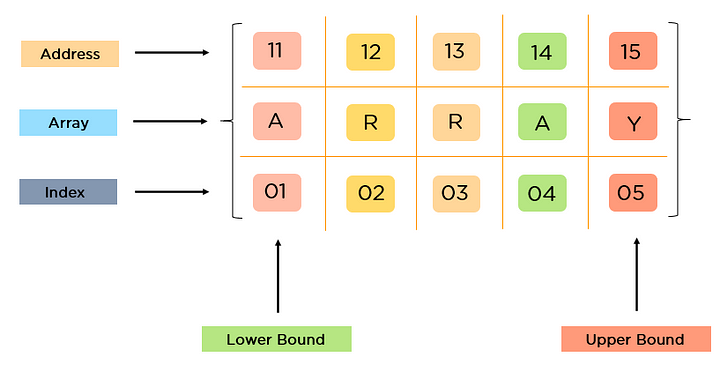
- 元素按順序連續(xù)存儲。
- 利用索引可以計算出元素對應的地址。
Array
- 一維數(shù)組——元素是線性存儲的,可以通過指定數(shù)組中存儲的每個元素的索引值來單獨訪問
- int a[n],string a[n]
- 多維數(shù)組——具有多個維度的數(shù)組
- int a[m][n],string a[m][n]
特征
- 所請求的內存空間的大小是固定的并且不能改變。使用前必須提前申請內存空間。
- 數(shù)組實現(xiàn)數(shù)學向量和矩陣,以及其他類型的矩形表。
優(yōu)點
- 按索引讀取效率高(支持隨機訪問應用)
- 搜索:時間復雜度為O(1)
缺點
- 寫入效率低(刪除和插入效率比較低,因為取決于插入和刪除的位置,需要做大量的數(shù)據(jù)移動,除非插入和刪除的位置是最后一位
- 插入/刪除:時間復雜度為O(n)
鏈表(Linked List)
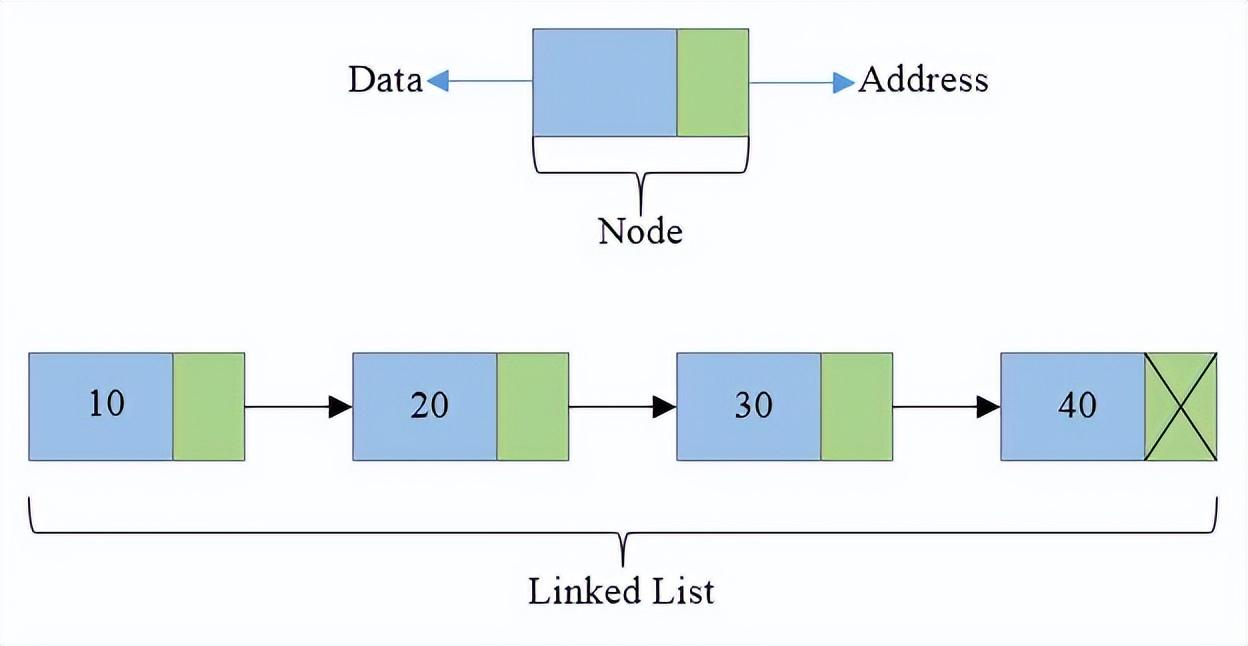
- 它是一種鏈式存儲結構,其中前一個元素的引用指向下一個元素,鏈表通過指針將元素與元素連接起來。所以,它不是按順序實現(xiàn)的,而是用指針實現(xiàn)的。
- 鏈表由一系列節(jié)點組成(每個節(jié)點由2部分組成:一個是存儲數(shù)據(jù)元素的數(shù)據(jù)字段,另一個是存儲下一個節(jié)點地址的指針字段
- 單鏈表、雙向鏈表和循環(huán)鏈表
- 鏈表中元素的插入和刪除比較簡單,因為不需要移動元素和實現(xiàn)長度擴展,但查詢一個元素比較困難
- 搜索:時間復雜度為O(n)
- 插入/刪除:時間復雜度為O(1)
優(yōu)點
- 可以任意添加或減少元素。
缺點
- 包含大量的指針字段,占用內存空間大
堆棧(Stack)
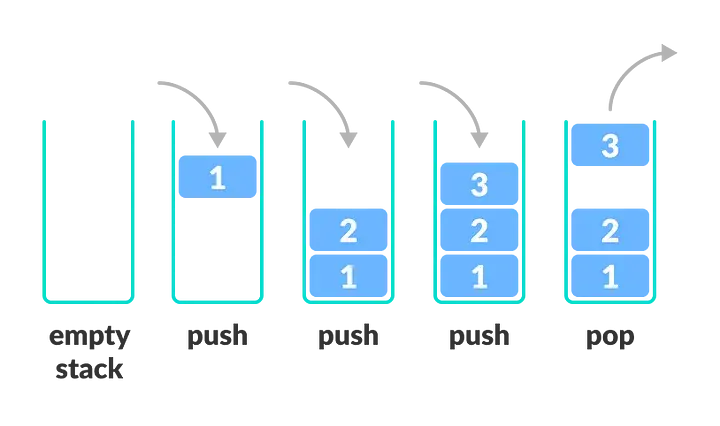
Stack
- 它是一種特殊的線性表,只能在一端插入和刪除。
- 它按照后進先出(LIFO)的原則存儲數(shù)據(jù)。
- 最先輸入的數(shù)據(jù)被壓入棧底,最后一個數(shù)據(jù)元素在棧頂。
- 最后一個數(shù)據(jù)元素首先被讀出或從堆棧頂部彈出。
- 插入=Push
- 刪除=Pop
- 棧中元素個數(shù)為零=空棧
- 插入/刪除:時間復雜度為O(1)
隊列(Queue)
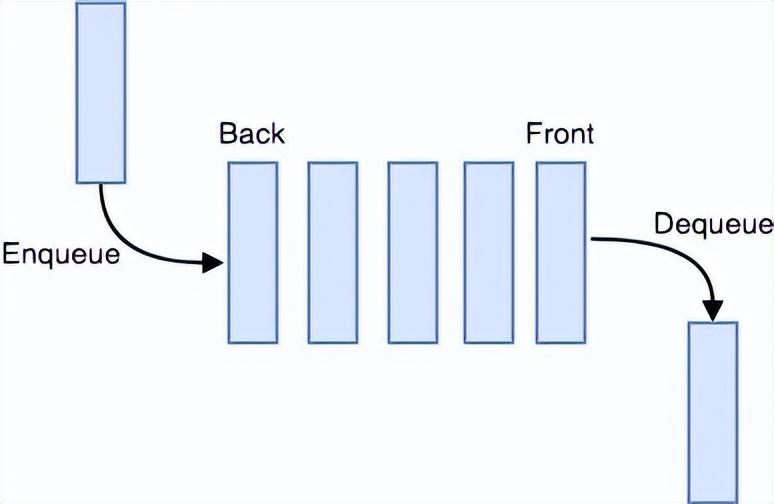
Queue
- 它是一個線性列表,允許在一端插入并在另一端刪除。
- 它的運行原理是先進先出(FIFO)
基本操作
Enqueue:向隊列中插入一個元素。
Dequeue:移除一個元素并返回隊列的第一個元素。
- 插入/刪除:時間復雜度為O(1)
- 循環(huán)隊列、優(yōu)先隊列
非線性
- 它是一種數(shù)據(jù)結構形式,其中數(shù)據(jù)元素不保持線性或順序排列
樹(Tree)
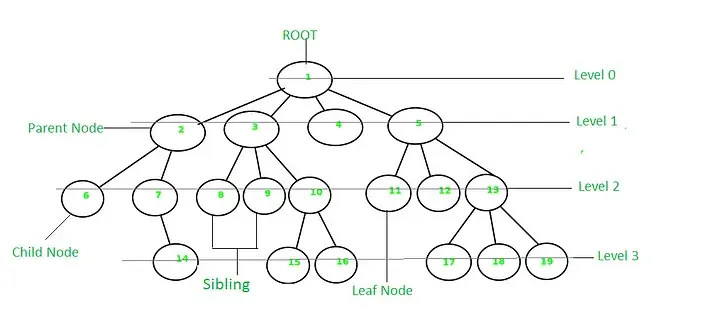
Tree
- 它是一種非線性存儲,由n(n≥1)個有限節(jié)點組成具有層次關系的集合
- 它顯示具有“一對多”關系的數(shù)據(jù)元素的集合
- 每個節(jié)點有零個或多個子節(jié)點
- 沒有父節(jié)點的節(jié)點=根節(jié)點
- 每個非根節(jié)點有且只有一個父節(jié)點
- 每個子節(jié)點可以分為多個不相交的子樹
- 節(jié)點深度=從根節(jié)點到x節(jié)點的路徑長度。根節(jié)點深度為0,第二層節(jié)點深度為1,以此類推
- 節(jié)點高度=葉子節(jié)點到x節(jié)點的路徑長度
- 節(jié)點的度=節(jié)點的子樹數(shù)量
- 葉節(jié)點= 度數(shù)為零的節(jié)點
二叉樹
- 每個節(jié)點最多有2個子樹,節(jié)點的最大度數(shù)為2
- 左子樹和右子樹是有序的,順序不能顛倒
- 即使一個節(jié)點只有1個子樹,也需要區(qū)分左右子樹
- AVL樹、紅黑樹、拉伸樹、替罪羊樹、B樹、B+樹、B*樹、字典樹(Trie樹)
哈希表(Hash table)
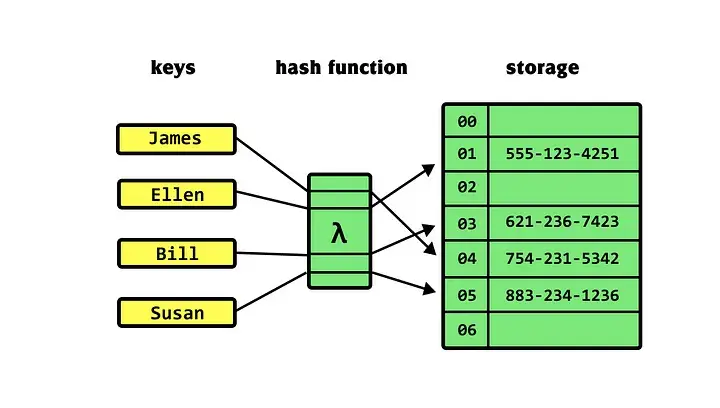
Hash table
- 它是一種根據(jù)映射函數(shù)直接訪問的特殊數(shù)據(jù)結構,以key:value的形式存儲數(shù)據(jù)。
- f(key) = 存儲位置。
- 哈希表就是通過哈希函數(shù)將唯一標識轉換成對應的位置。
- 查找、插入:時間復雜度為O(1)。
- 但是,如果哈希值都映射到同一個地址,則查找的時間復雜度為O(n)。
- 鏈接尋址——哈希函數(shù)將鍵值映射到哈希表中的每個位置。
- 開放尋址— 如果存在位置映射沖突,其中鍵 1 和鍵 2 共享相同位置,則將鍵 2 放入空空間并啟動尋找空閑位置的過程。
- 檢測方法 = 線性探測、二次探測、雙重散列。
堆(Heap)
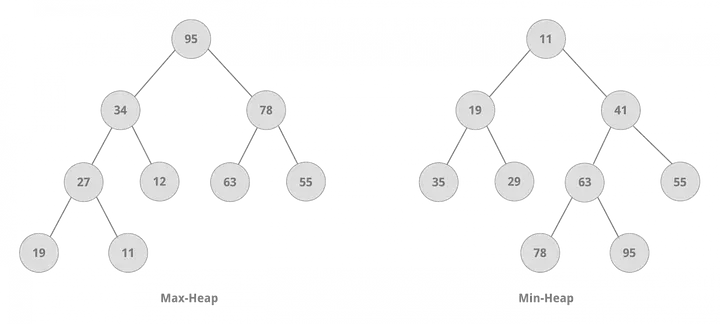
Heap
- 它是一個完全二叉樹。
- 它是一個圖樹結構,用于實現(xiàn)“優(yōu)先級隊列”。
- 堆中節(jié)點的值始終不大于或小于其父節(jié)點的值。
- Min Heap = 根節(jié)點最小的堆,滿足 ki ≤ K2i+1 且 ki ≤ k2i+2。
- Max Heap = 根節(jié)點最大的堆,滿足 ki ≥ k2i+1 且 ki ≥ k2i+2。
圖表(Graph)
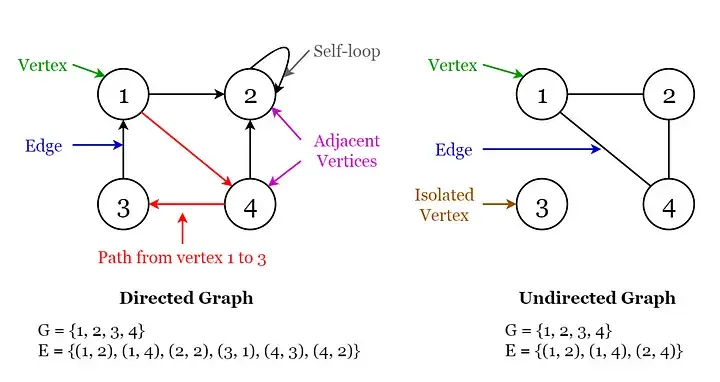
圖形術語的可視化
- 它是一種相對復雜的數(shù)據(jù)結構,具有相對復雜且高效的數(shù)據(jù)存儲算法。
- 它展示了對象與對象之間復雜的“多對多”關系。
- 它由有限的頂點集 V 和邊集 E 組成。
可分為無向圖和有向圖:
- (v,w)表示無向邊,即v和w是互連的。
- <v, w> 表示從 v 開始到 w 結束的有向邊。
圖可以分為加權圖和未加權圖:
- 加權圖:每條邊都有一定的權重,通常是一個數(shù)字。
- 無權圖:每條邊沒有權重,也可以理解為權重為1。
圖可以分為連通圖和非連通圖:
- 連通圖:所有點都通過路徑連接。
- 斷開圖:有兩個點沒有通過路徑連接。
圖中的頂點有度的概念:
- 度數(shù)——與其相連的所有點的總和。
- 入度 — 存在于有向圖中,訪問該點的所有邊的總和。
- 出度——存在于有向圖中,與該點相連的邊數(shù)之和。
圖表的表示
- 鄰接矩陣— 具有 n 個頂點的圖需要具有大小為 nxn 的矩陣。
- 鄰接表- 具有鏈表數(shù)組的圖。
- 算法:圖的搜索算法、廣度優(yōu)先搜索(BFS)、深度優(yōu)先搜索(DFS)等。
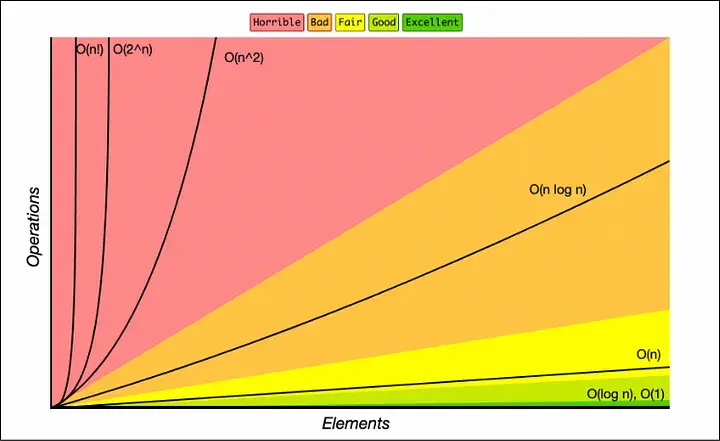
大O復雜性
責任編輯:姜華
來源:
今日頭條